Mit freundlicher Genehmigung des Autors Klaus Wittlich.
Der folgende Text: © Copyright 1991-2002, Klaus Wittlich. Erstmals erschienen in der Schrift KANN DER NEODARWINISMUS DURCH BIOLOGISCHE TATSACHEN WIDERLEGT WERDEN? (Naturwissenschaftlicher Verlag Köln, 1991).
Ich betrachte die Problematik der Evolution aus der Sicht des Programmierers. Man kann den genetischen Code als ein riesiges Programm auffassen, welches sich aus verschiedenen Unterprogrammen zusammensetzt, die in DNA-Sequenzen gespeichert sind. Ich möchte nun die Wahrscheinlichkeit untersuchen, mit der funktionstüchtige „Unterprogramme“ durch Mutation und Selektion entstehen können. Angeregt zu diesen Überlegungen wurde ich durch Dr. W.-E. Lönnig und die Vorstellung, meine Katze über meine Computertastatur laufen zu lassen und so durch zufällige Änderungen meine Programme zu verbessern. Die Frage war nun, wie oft und wie lange ich das tun müsste, bis ich endlich bessere Programme erwarten kann. Zufällige Mutationen werden durch das Herumtreten der Katze simuliert und ich als Mensch kann dann sehen, ob die Programme besser geworden sind (überlebensfähiger) oder schlechter und somit eine Art Selektionsdruck erzeugen. Programme, die die Katze verbessert hat, können weiterbearbeitet werden, Programme, die verschlechtert worden sind, scheiden aus dem Daseinskampf aus, Programme, die weder besser noch schlechter geworden sind, werden wie ihre Vorgänger behandelt.
Von der Programmierlogik her ist klar, dass Unterprogramme erst dann etwas nützen, wenn sie fertig und damit funktionstüchtig sind, sonst nicht. Das Prinzip der Evolution der kleinen Schritte („wieder ein richtiges Zeichen gefunden, das Unterprogramm ist also besser geworden“) ist daher nicht anwendbar. Die Unterprogramme im biologischen Sinn sind funktionstüchtige DNA-Ketten. Die Anzahl der möglichen DNA-Ketten einer bestimmten Länge sind nun zu berechnen.
Im Folgenden möchte ich zeigen, wie man die Vielfachheiten einer DNA-Kette ausrechnet.
Wir betrachten einen Strang der Länge 0. Es gibt nur einen Strang der Länge 0, also insgesamt 40 = 1 Möglichkeiten. Wir haben nun 4 Möglichkeiten, eine Base an den leeren Strang anzuhängen und haben damit 41 = 4 · 40 Möglichkeiten für einen Strang der Länge 1. Ein Strang der Länge 2 entsteht, wenn man an einen Strang der Länge 1 eine Base anhängt. Man hat zu jedem möglichen Strang der Länge 1 4 Möglichkeiten, also insgesamt 41 · 4 = 42 = 16 Möglichkeiten. Einen Strang der Länge 3 erhält man, indem man an einen Strang der Länge 2 eine Base anhängt. Zu jedem der bisherigen 42 Möglichkeiten gibt es vier Möglichkeiten, eine Base anzuhängen, also damit insgesamt 4 · 42 = 43 = 64 Möglichkeiten. Verallgemeinerung des Verfahrens liefert: Für einen Strang der Länge n gibt es 4n Möglichkeiten. Für einen Strang, der aus 1250 Basen besteht (viele Gene sind wesentlich länger), rechnen wir zunächst die etwa 20 % Basenaustauschmutation ab, die wegen des degenerierten Codes ein neues Gleichsinncodon und damit den Wildtyp bilden. Tausend Basen sind dann unser Ausgangspunkt für die weiteren Berechnungen 41000 = 1,15 · 10602 Möglichkeiten, also eine 603-stellige Zahl.
An diesem Punkt wird man nun einwenden, dass die Evolution ja reichlich Zeit gehabt hat, zu experimentieren, und während einer so langen Zeitspanne kann nun ja doch etwas Brauchbares sich ergeben. Rechnen wir das nach, indem wir der Evolution dabei sogar mehr Zeit zur Verfügung stellen, als sie tatsächlich hatte. Das Alter des Universums wird auf 10 Mrd Jahre geschätzt. Wir machen eine Billion = 1012 Jahre daraus. Ein Jahr hat 365 Tage, wir geben einem Jahr 1000 = 103 Tage. Ein Tag hat 86400 Sekunden, wir verlängern ihn auf 100000 = 105 Sekunden. Die Dauer einer Generation setzten wir auf eine Sekunde runter. Damit geben wir der Evolution mehr Generationen, als sie tatsächlich hatte. Wir kommen auf 1012 · 103 · 105 = 1020 Sekunden bzw. Generationen. Damit müssen, damit man mit einem brauchbaren Strang während der Geschichte des Universums rechnen kann, pro Sekunde mindestens 1,15 · 10602 / 1020 = 1,15 · 10582 Versuche stattfinden.
Weiterer Punkt: Auf der Erde existiert aber nicht nur ein Individuum zu einer bestimmten Zeit, es werden ja viele Experimente gleichzeitig gemacht. Dazu schätzen wir die Anzahl der möglichen Individuen ab. Es kann auf keinen Fall mehr Individuen/Experimente als Atome geben. Die Masse der Erde geteilt durch die Masse des Wasserstoff-Atoms liefert:
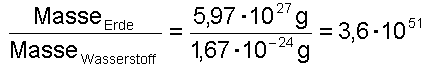
Damit ergibt sich für die Zahl der pro Sekunde seit Entstehung des Universums pro Atom der Erde benötigten Versuche zu
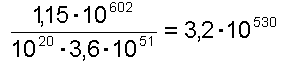
um mit einem (!) brauchbaren 1000-Basen-DNA-Strang rechnen zu können.
Weiterer Einwand: Bisher waren das ja alles statistische Überlegungen. Aber das etwas schrecklich unwahrscheinlich ist, heißt ja noch nicht, dass etwas unmöglich ist. So ein unwahrscheinliches Ereignis kann doch stattgefunden haben. Außerdem ist ein Schöpfer eine metaphysische Größe und in einem Modell höchst unbefriedigend.
Man kann auch die Entstehung eines Hauses damit erklären, dass ein Orkan über einen Trümmerhaufen fegt und die neue Anordnung des Trümmerhaufens ein Haus ist. Dieses Ereignis ist sehr unwahrscheinlich, aber möglich, jedoch wegen seiner geringen Wahrscheinlichkeit bisher nicht beobachtet worden. Man kann sich also beruhigt für die Trümmerhaufentheorie einsetzen, wenn man will, man muss sich lediglich über die Statistik hinwegsetzen. Außerdem hat die Trümmerhaufentheorie den Vorteil, dass man nicht so unbefriedigende metaphysische Größen wie Architekten, Bauleute und Kranführer oder sonstige Intelligenzen heranziehen muss.
Ein weiterer Einwand ist, dass nun nicht alle Basen exakt stimmen müssen. Es gibt Fälle, wo bis zu einigen Prozent Abweichungen vom Original möglich sind, und der DNA-Strang dennoch funktioniert.
Dazu müssen wir uns überlegen, wie viele Basenstränge einer bestimmten Länge n möglich sind, wobei genau k falsch ist. Betrachten wir dazu folgendes Diagramm:
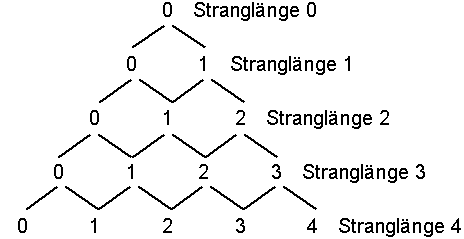
Zweck des Diagramms ist es, die Zahl der möglichen Ketten der Länge n zu bestimmen, bei der genau k Basen falsch sind. Hat man bereits einen Strang der Länge n, bei der k Basen falsch sind, und hängt dann eine weitere Base an, so hat man entweder einen Strang der Länge n + 1, bei dem k Basen falsch sind, wenn man die eine richtige angehängt hat, oder man hat k + 1 Möglichkeiten, wenn man eine von den drei falschen Basen angehängt hat. Die eine richtige Möglichkeit ist im Diagramm durch / und die drei falschen Möglichkeiten durch ein \ gekennzeichnet. Damit entspricht jeder „Zustand“ der Länge n mit genau k falschen Basen einem Punkt im Diagramm. Eine Sequenz mit 3 Basen, wobei 2 falsch sind, steht in Zeile 3 (Stranglänge 3) an der zweiten Stelle. (Zu beachten: Die Zählung beginnt bei 0). Um zu diesem Punkt zu gelangen, muss man 2x in Richtung falsch (\) und einmal in Richtung richtig (/) gegangen sein. Ein Schritt in Richtung falsch bedeutet einen Faktor von 3, wir sind 2 solche Schritte im Diagramm gegangen, also erhalten wir dadurch einen Faktor 3 · 3 = 32. Ein Schritt in Richtung richtig bedeutet einen Faktor 1, wir sind einen Schritt in diese Richtung gegangen, also kommt ein Faktor 11 hinzu. Unserem Produkt fehlt jetzt nur noch der Faktor „Anzahl der möglichen Wege zu dem Punkt“. Diesen kann man sich nun wie folgt überlegen: Um zum Punkt „2 von 3 falsch“ gekommen zu sein, muss man entweder über den Punkt „1 von 2 falsch“ oder über den Punkt „2 von 2 falsch“ gelaufen sein. Dieses Additionsschema ist aber genau das Additionsschema des PASCALschen Dreiecks, und damit ist die Anzahl der Wege genau gleich den Koeffizienten des PASCALschen Dreiecks. Man schreibt für den Koeffizienten in der n-ten Zeile (Stranglänge n) und der k-ten Spalte (k falsch):
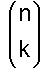
Dieser Koeffizient heißt Binomialkoeffizient und berechnet sich wie folgt (ohne Beweis):
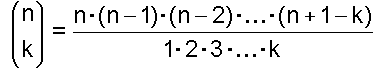
(Beachte: Zähler und Nenner haben jeweils die gleiche Anzahl Faktoren.) und für k = 0 definiert man:
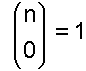
Damit ergibt sich als abschließende Zahl für genau k falsche Basen von n:
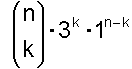
Wenn bis zu k Basen falsch sein sollen, dann muss man die Möglichkeiten für genau 0 falsch und genau 1 falsch und … und genau k falsch zusammenzählen und erhält:
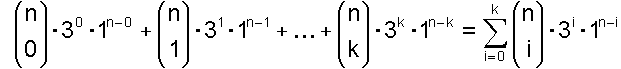
Von Interesse ist das Verhältnis von allen möglichen Nukleinsäuresträngen zum Verhältnis der günstigen Nukleinsäuresträngen. Dieses ist:
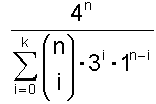
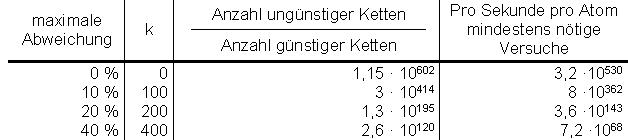
Mit dieser Formel erhält man dann schließlich folgende Tabelle für einen Nukleinsäurestrang der Länge n = 1000:
Prof. K. schreibt (Biologie heute, 1990, p. 8): „Kritiker sagen, neue Taxa benötigen neue Funktionen und Strukturen und also neue DNS-Sequenzen. Diese könnten aber nicht durch Zufälle entstehen, denn schon die Zufallschance für eine DNS-Sequenz aus 1000 Gliedern sei nur 4-1000 = 10-602 und im All nicht realisierbar. Diese immer wieder vorgebrachte Rechnung ist aber unzutreffend. Denn eine Funktion, z.B. Enzymaktivität, kann durch sehr viele Sequenzvarianten entstehen, nicht nur durch eine einzige, wie die Rechnung voraussetzt. Sequenzvergleiche „derselben“ Enzyme verschiedener Spezies zeigen, dass nur wenige Glieder einer Sequenz für eine Funktionsfähigkeit bestimmt besetzt sein müssen, die übrigen können ziemlich frei, z.T. sogar ganz zufällig gewählt sein. Dadurch kann jene Chance bei 10-5 bis 10-7 liegen.“
Wie der Leser erkennt, liefert der vorliegende Ansatz nicht nur eine einzige Sequenzvariante, sondern sehr viele: Selbst bei 40% maximaler Abweichung ein Wert, der für die meisten Enzyme bereits völlig irrelevant sein dürfte, ist die pro Sekunde pro Atom der Erde seit Entstehung der Universums nötige Zahl an Versuchen 7,2 · 1068. Bei einer zulässigen Abweichung bis 40 % gibt es 1,15 · 10602 / 2,6 · 10120 = 4,5 · 10481 brauchbare Möglichkeiten, bei einer zulässigen Abweichung von genau 40 % gibt es „nur“ noch 5 · 10290 Varianten.
